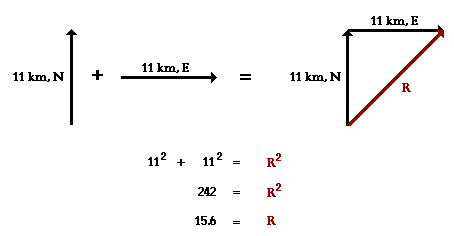Modulul Sumei A Doi Vectori

V 1 v 2 x 1 x 2 i y 1 y 2 j produsul unui vector cu un scalar.

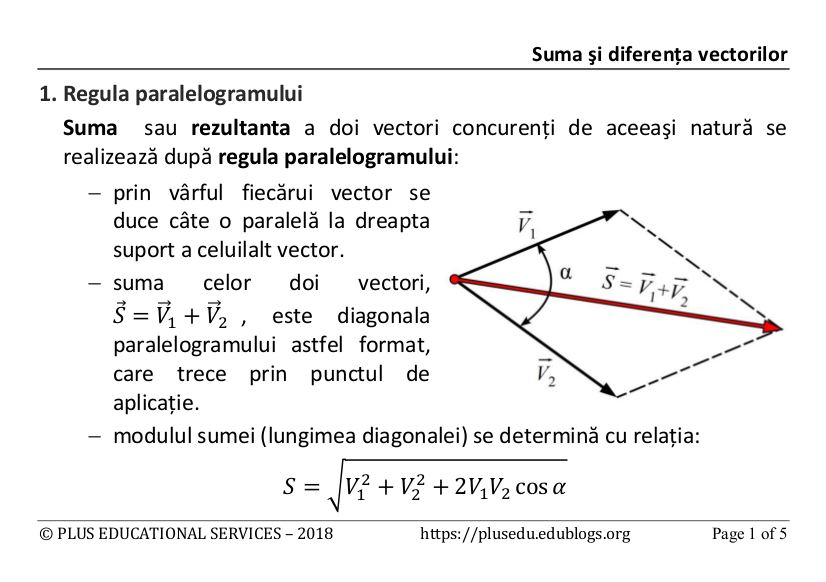
Modulul sumei a doi vectori. Adunarea mai multor vectori după regula patrulaterului. 9 calculul cu vectori liberi poate fi folosit în rezolvarea unor probleme de geometrie unele chiar foarte rezistente la o abordare directă. Adunarea a doi vectori după regula paralelogramului. Aplica formula stiind valorile lui cos de 30 60 90 si 180 de grade aplica formula stiind valorile lui cos de 30 60 90 si 180 de grade.

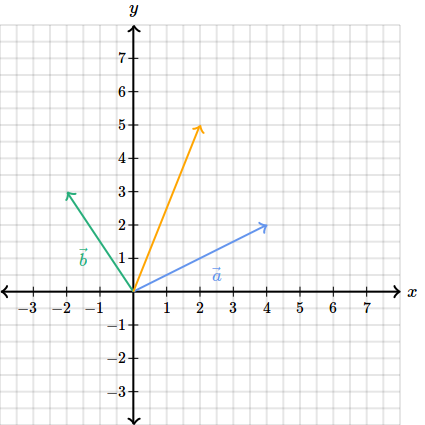
Numărul se numește produsul scalar al vectorilor și și este egal cu produsul dintre modulul vectorului modulul vectorului și cosinusul unghiului dintre cei doi vectori. Vom lua pe rând aceste cazuri și le vom discuta. Adunare a doi sau mai mulți vectori se face după anumite reguli astfel că avem trei cazuri. Modul de definire a sumei vectorilor face posibilă descompunerea unui vector după două direcţii necoliniare în plan sau după trei direcţii necoplanare în spaţiu.

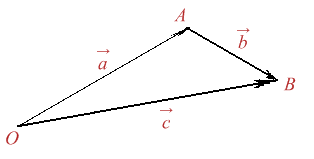
V 1 v 2 x 1 x 2 y 1 y 2 v 1 v 2 v 1 v 2 c o s v 1 v 2 modulul lungimea unui vector u a i b j este u a 2 b 2. Adunarea a doi vectori după regula triunghiului. Observatie numele acestui produs de vectori vine din faptul ca. Unde este masura unghiului celor doi vectori 2 0 ˇ daca unul dintre vectori este 0 produsul lor scalar este prin de nitie 0.

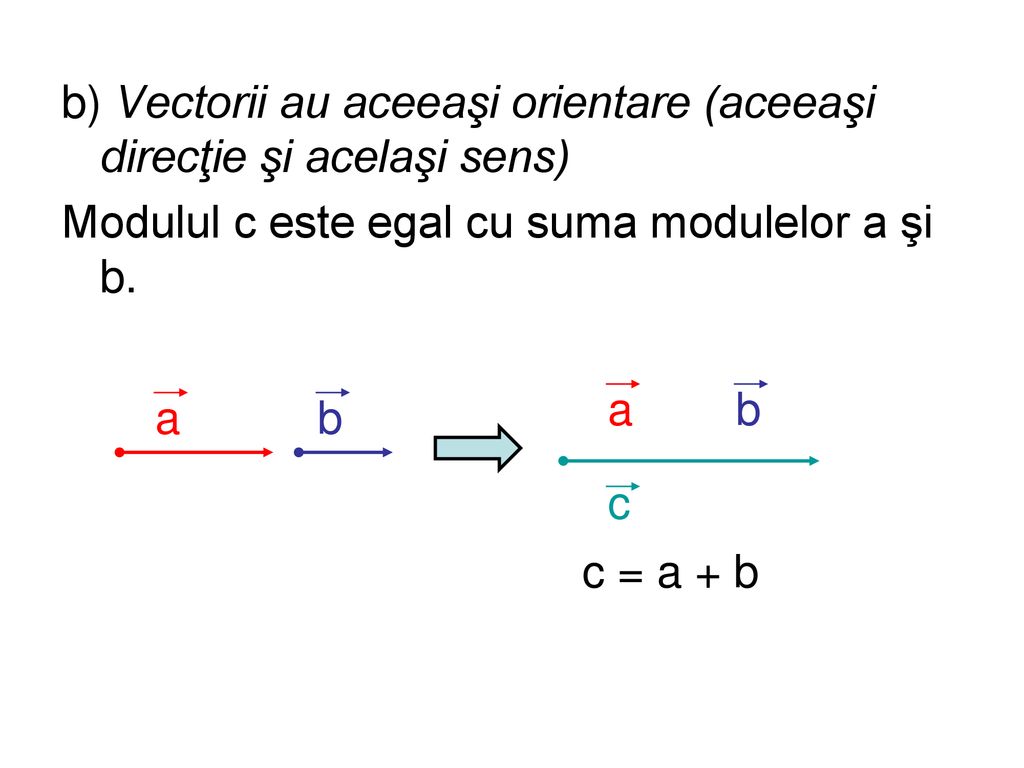
Fie vectorii liberi nenuli u v 2v. Produsul scalar al celor doi vectori se noteaza cu u v sau u v. U v si se de neste prin u v ju jjv jcos. Modulul rezultantei a doi sau mai multi vectori care au aceeasi directie si sensuri opuse se obtine prin scaderea lungimilor vectorilor daca se obtine o valoare negativa se alege pentru vecorul rezultant un sens opus.

Modulul sumei a doi vectori este dat de expresia s v1 v2 2v1v2cos α.